電子相関や乱れで金属絶縁体転移が駆動されますが、実はこの2種類の絶縁体は互いに異なる1粒子励起構造を持つことが知られています。つまり、電子相関が駆動する絶縁体は1粒子状態密度(スペクトル関数、以下単に状態密度と書きます)におけるギャップで特徴付けられていて、基底状態にキャリアを1個付け加えるには有限のエネルギーが必要です。例えば、モット絶縁体におけるモットギャップはその典型です[3]。一方、乱れによって散乱されたキャリアが量子的に干渉し定在波を作ることで生じるアンダーソン絶縁体では、モット絶縁体とは対照的に状態密度はフェルミエネルギー上で有限の値を持ちギャップはありません[4]。
現実の物質では乱れと電子間相互作用双方の影響を無視できず、電子相関と乱れが共存していると見なさざるを得ない場合が多くあります。例えばドープされた半導体の低濃度領域では乱れによるアンダーソン局在が起きていますが、一方で電子間相互作用の遮蔽が弱く長距離クーロン力の影響も強いと考えられます。このような場合にはどのようなギャップ構造が現れるのでしょうか?EfrosとShklovskiiは、アンダーソン絶縁体において、基底状態から励起された電子-ホール対間に働く長距離クーロン力の効果を理論的に考察しました。その結果、電子-ホール励起に対する基底状態の安定性から低エネルギー1粒子励起状態が排除され、状態密度にソフトギャップが形成されることを示したのです[5]。ここで、ソフトギャップとはフェルミエネルギー上でのみ状態密度が0となる構造であり、乱れや長距離クーロン力単独の効果では説明できないものです。この励起構造の変化は物性に強く影響し、例えば電気伝導度は、通常のアンダーソン絶縁体が従うモット公式や、有限のギャップがある場合の熱励起型とは異なる温度依存性を持ちます[5]。
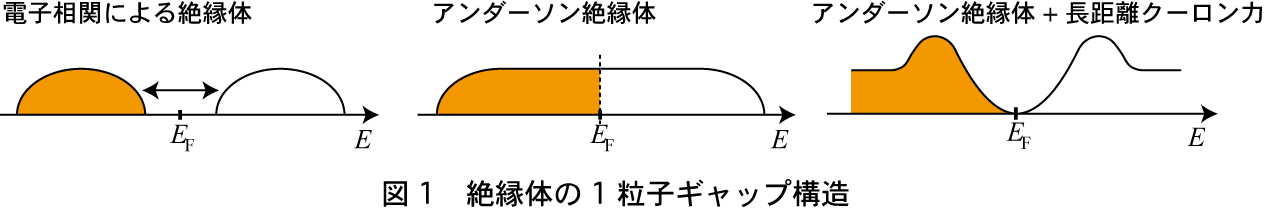
一方、近年注目を浴びている遷移金属酸化物などの強相関電子系では、半導体に比べて遮蔽が強く相互作用はむしろ短距離的であると考えられています。この場合、励起された電子-ホール対間の長距離相互作用は無視できるため、従来の理論ではソフトギャップは現れません。ところが、近年短距離相互作用模型である3次元アンダーソン・ハバード模型において、ソフトギャップの形成が数値的に報告されました[6]。アンダーソン・ハバード模型とは、オンサイト斥力を含むハバード模型に乱れとしてランダムポテンシャルを導入した模型です。この結果は新しいソフトギャップの機構の存在を示唆するものですが、その機構は未解明でした。また、励起状態を理解するには、それと表裏一体の関係にある基底状態の相図を系統的に求める必要があります。しかし、解析に用いられたハートリー・フォック近似は空間的に不均一な平均場を用いる手法であり、大変計算量が多いという問題があります。そのため基底状態の相図の全容は明らかにされていませんでした。
そのため、私たちは3次元アンダーソン・ハバード模型にハートリー・フォック近似を適用しました。その結果、1. スーパーコンピュータや後述の大規模数値計算技法を用いて基底状態の相図を決定し、2. 励起構造に関して別途構築した現象論と詳細に比較することでソフトギャップの起源を解明しました。以下ではそれぞれ2つの結果を簡単に紹介します。
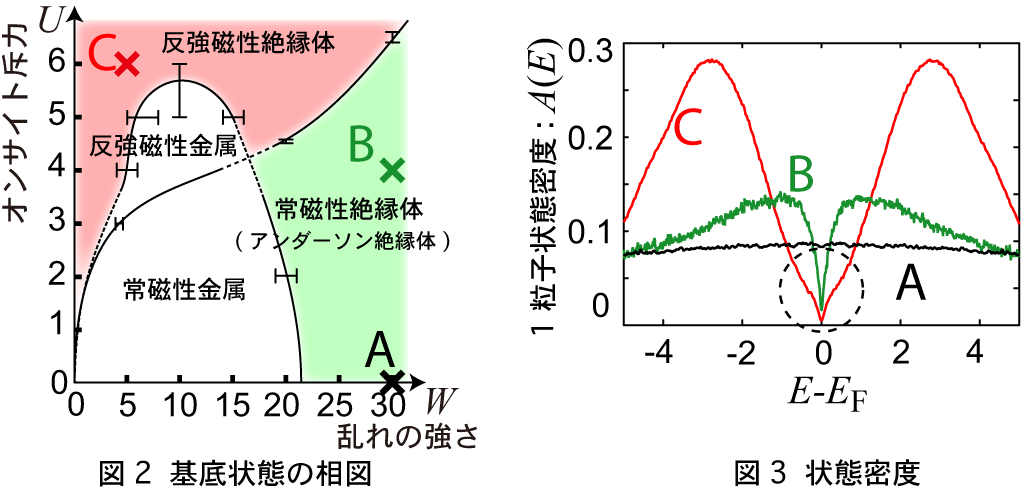
まず、3次元正方格子上のアンダーソン・ハバード模型の基底状態の相図を求めました (図2、エネルギー単位は最近接ホッピング)。ここでWはランダムポテンシャルの分布幅に比例する乱れの強さのパラメータです。オンサイト斥力Uが強い場合には反強磁性絶縁体、乱れが強い場合にはアンダーソン絶縁体が現れます。一方、乱れと電子相関が共に弱い領域に 金属相は限られています。
次に、絶縁相における励起構造を解析しました (図3)。電子相関のないアンダーソン絶縁体に対応するA点(図2)では、確かに状態密度にギャップはありません。ここで、E, EF, A(E)はそれぞれエネルギー、フェルミエネルギー、状態密度を表します。ところが、電子相関と乱れが共存する絶縁相では、B, C点に見られるように、電子相関効果によって低エネルギーの局在準位が排除されソフトギャップが形成されています。我々は、短距離相互作用から形成されるこのソフトギャップをソフトハバードギャップと呼ぶことにしました。また、1、2次元において同様の計算を行い、ソフトハバードギャップの形成を確認しました。さらに、1次元において厳密対角化法を適用し、平均場近似を超えてもソフトハバードギャップが形成されることを示唆する結果を得ました。
私たちは位相空間におけるエネルギーの複雑な多谷構造を仮定することでソフトハバードギャップの形成が理解できることを明らかにしました。乱れに起因するこの多谷構造の下では、基底状態とほとんどエネルギーは縮退しているものの、電子状態は全系に渡って異なっているような励起状態が多数存在します。電子―ホール励起の代わりに、このような集団的な低エネルギー励起に対する安定性を考えることで、状態密度A(E)のエネルギーEに対する以下のスケーリング則を導くことができます。ここで、dは空間次元、γは正のnon-universalな定数です。この式は、3次元において状態密度が冪則よりも早くフェルミエネルギーに向かって減少することを示しています。実際、B, C点における状態密度の数値データはフェルミエネルギー近傍でよくスケーリング則に従うことが分かりました(図4)。
近年、従来の長距離クーロン力による理論が予測するスケーリング則 に従わないソフトギャップが複数の物質で観測されています[7]。これらの物質は誘電率が発散する金属絶縁体転移近傍に位置するので、遮蔽が強く短距離相互作用が支配的だと期待されます。実際、SrRu1-xTixO3の実験結果 (光電子分光、電気伝導度の温度依存性)を私たちの短距離相互作用に対する理論と比較し、無矛盾であることを示しました。

ランダム系の電子状態では空間相関が重要な役割を担っています。しかし、空間相関を取り込めるもっとも素朴なハートリー・フォック近似の範囲ですら、1.多数の準安定状態が存在するために基底状態探索が困難であり、2.乱れの効果を取り込む為には大きなスーパーセルを取り扱う必要があるなどの理由で従来は系統的な計算が難しかったのです。その点、基底状態を系統的に探索する方法を考案し、並列化、オーダーN法などの種々の大規模系の計算技法を駆使することで困難を乗り越えることに成功しました。さらに、多谷構造という概念を提唱し、その上で従来の理論で考慮された電子-ホール励起のような局所的な励起ではなく、集団的な励起を考えることで計算結果を説明したことも独創的な点だと考えています。多谷構造はスピングラスの分野でもその存在が議論されていますので、さらなる理論研究の発展が期待されます。また、本研究の結果が短距離相互作用が支配的な強相関電子系の物性を理解する上で重要な理論基盤となることを期待しています。